Nella prima parte ho dimostrato come si possono ottenere con dei semplici calcoli alcune proprietà di un ipotetico pianeta in orbita ad una stella remota. La parte più difficile è però calcolare la massa dell’esopianeta, una sfida difficile ma ricca di soddisfazioni.

La Seconda Legge del Moto di Newton e la Legge di Gravitazione Universale mostrano che esiste un elegante rapporto tra il semiasse maggiore dell’orbita e il periodo di rivoluzione di un qualsiasi pianeta.
Di conseguenza, conoscendo esattamente il periodo orbitale e la distanza che divide un pianeta dal suo centro di massa con la stella a cui appartiene è possibile estrapolarne la massa:
![]()
Pertanto osservando le leggi universali del moto e della gravitazione di Newton potrebbe sembrare che sia abbastanza semplice estrapolare la massa di un esopianeta 1; quello che occorre è la conoscenza più accurata possibile degli elementi orbitali dell’esopianeta.
La distanza prospettica tra la proiezione della corda di transito e la corda del massimo transito è descritta matematicamente come ![]() , dove
, dove ![]() è il raggio dell’orbita del pianeta, assumendo per assurdo che l’orbita dell’esopianeta osservato sia perfettamente circolare (
è il raggio dell’orbita del pianeta, assumendo per assurdo che l’orbita dell’esopianeta osservato sia perfettamente circolare (![]() e velocità orbitale costante). Osservando la figura qui sotto si nota che il cateto
e velocità orbitale costante). Osservando la figura qui sotto si nota che il cateto ![]() opposto all’ipotenusa
opposto all’ipotenusa ![]() e pari alla metà del percorso del pianeta davanti alla sua stella, lo si può scrivere come :
e pari alla metà del percorso del pianeta davanti alla sua stella, lo si può scrivere come :
![]()
.
Pertanto il percorso osservato del’esopianeta (A -> B) sul disco stellare è pari a 2![]() .
.
Osservando la figura all’inizio è evidente che l’esopianeta mentre transita davanti alla stella muovendosi tra A a B compie un angolo (espresso in radianti) ![]() dove il centro è il centro di massa del sistema 2.
dove il centro è il centro di massa del sistema 2.
Così si ha per il triangolo ![]() e il centro di massa, la durata visibile del transito:
e il centro di massa, la durata visibile del transito:
![]()
![]()
![Rendered by QuickLaTeX.com \[ D_{transito}= P\frac{\alpha}{2\pi}=\frac{P}{\pi}sin^{-1} \left(\frac{l}{a}\right)=\frac{P}{\pi}sin^{-1} \left(\frac{\sqrt{\left( R_{\bigstar} + R_{p}\right)^2 - b^2 }}{a}\right) \]](http://drake.ilpoliedrico.com/wp-content/ql-cache/quicklatex.com-2feb8bc7ceae9d8c8bea1ccacda32021_l3.png)
Per procedere oltre, occorre stimare la durata massima del transito, come se si osservasse il piano orbitale proprio di taglio, quando il pianeta cioè attraversa la stella sul suo equatore. Infatti la durata del transito osservato è generalmente minore rispetto a quella massima possibile che si avrebbe solo quando il piano planetario è parallelo all’osservatore, data la casualità dei piani planetari delle altre stelle rispetto all’osservatore.

Credit: Il Poliedrico
Come è possibile osservare nella figura qui sopra la proiezione del pianeta sul disco stellare è falsata dall’angolo ![]() , inteso come l’angolo compreso tra la linea di vista e il piano orbitale effettivo dell’esopianeta (
, inteso come l’angolo compreso tra la linea di vista e il piano orbitale effettivo dell’esopianeta (![]() =90° se il piano orbitale è sulla stessa linea di vista). Conoscere l’ampiezza dell’angolo
=90° se il piano orbitale è sulla stessa linea di vista). Conoscere l’ampiezza dell’angolo ![]() restituisce l’idea di come è pertanto posizionato nello spazio il sistema planetario extrasolare rispetto all’osservatore. Quindi in realtà la durata del transito osservata sarà pari a
restituisce l’idea di come è pertanto posizionato nello spazio il sistema planetario extrasolare rispetto all’osservatore. Quindi in realtà la durata del transito osservata sarà pari a ![]() . Ma non solo, come è possibile osservare nella simulazione qui a fianco, lo sviluppo del transito su una corda diversa dalla corda massima (il diametro) influenza anche la curva di transito osservata, accorciando il periodo del picco minimo osservabile e stirando i periodi parziali [1].
. Ma non solo, come è possibile osservare nella simulazione qui a fianco, lo sviluppo del transito su una corda diversa dalla corda massima (il diametro) influenza anche la curva di transito osservata, accorciando il periodo del picco minimo osservabile e stirando i periodi parziali [1].
Adesso la durata massima del transito si può descrivere matematicamente come:
![]()
perché la lunghezza della corda di transito è falsata (e quindi minore) rispetto alla corda massima disponibile dal ![]() .
.
Quindi applicando la legge dell’anno siderale di Gauss si scopre che:
![]()
![]()
![]()
Il periodo orbitale rilevato dalla frequenza dei transiti restituisce la durata dell’anno siderale reale, ovvero quello che è prodotto con il contributo delle due masse, quella stellare e quella planetaria. Viceversa l’anno gaussiano del pianeta tiene conto solo della massa della stella. La differenza tra i due diversi periodi restituisce il contributo dovuto alla sola massa del pianeta.
| [showmap name=’RoquedeLosMuchachos_’] |
La tecnologia osservativa attuale basata sui transiti non è ancora così precisa da consentire di rilevare differenze così piccole 3. Diversa storia invece per l’analisi spettrografica che consente con molta maggiore accuratezza di risolvere le velocità relative del sistema esoplanetario; per ora rimane infatti il solo modo per stabilire con sufficiente approssimazione la massa di un pianeta extrasolare.
Per questo strumenti spettroscopici di grandissima risoluzione sono ospitati nei maggiori complessi astronomici del mondo. Due di questi, gli HARPS sono ospitati in strutture europee: l’HARPS-S è ospitato presso l’Osservatorio di La Silla, in Cile sul telescopio da 3,6 metri dell’ESO fin dal 2002. L’altro, l’HARPS-N, è stato montato nel 2012 sul Telescopio Nazionale Galileo, all’Osservatorio del Roque de Los Muchachos nell’isola di La Palma, alle Canarie.
Il metodo delle velocità radiali rilevate spettroscopicamente è molto simile a quello che qui è descritto, solo che è molto più efficace grazie a questa nuova classe di spettroscopi ultra precisi a cui gli HARPS appartengono. Se adesso è possibile fare una stima della massa ad un esopianeta lo si deve ad essi.
Note:
Note:
- In realtà incertezze sulla misura della massa della stella, dei dati orbitali effettivi e l’enorme differenza tra le masse in gioco rendono il calcolo molto più complesso e soggetto a errori. ↩
- Un’orbita idealmente circolare è descritta come
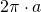 dove
dove  è il raggio dell’orbita. ↩
è il raggio dell’orbita. ↩ - Ad esempio la massa del Sole è 330 000 volte quella della Terra. ↩
Riferimenti:
- K. Mandel, and E. Agol, "Analytic Lightcurves for Planetary Transit Searches", arXiv, 2002. http://arxiv.org/abs/astro-ph/0210099
